matlab 与神经网络 (3)

定义及特性

　　竞争型神经网络是基于无监督学习(unsupervised learning)方法的一种神经网络．

　　竞争型神经网络模型如下

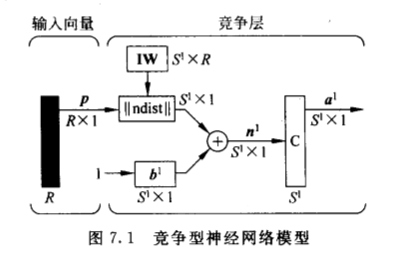
　　可以看出竞争性神经网络为单层网络． $$\mid \mid ndist \mid \mid$$的输入为输入向量 p 和输入权值向量 $$\bf{IW}$$, 其输出为 $$S^1 \times 1$$ 的列向量，列向量中每个元素为输入向量 p 和输入权值向量 $$\bf{IW}$$ 的距离的负数，在神经网络工具箱中以距离函数 negdist 计算．

　　$$n^1$$ 为竞争层传输函数的输入，其值为输入向量 p 和输入权值向量 $$\bf{IW}$$ 距离的负数与阈值 $$b^1$$ 之和．如果所有的阈值向量为 0, 则当输入向量 p 和输入权值向量 $$\bf{IW}$$ 相等时，$$n^1$$ 为最大值 0.

　　对于 $$n^1$$ 中的最大的元素，竞争层传输函数输出 1(即竞争的”获胜者”输出为1)，而其他元素均输出 0, 如果所有的阈值向量为 0, 则当神经元的权值向量最接近输入向量时，它在 $$n^1$$ 各元素中的负值最小，而值最大，从而赢得竞争，对应的输出为 1.

　　以 newc 创建竞争性神经网络，其权值的初始化函数为 midpoint, 阈值的初始化函数为 initcon.

竞争性神经网络的学习

1. Kohonen 权值学习规则，以 learnk 函数实现

   　　假若第 i 个神经元获胜，则输入权值向量的第 i 行元素(即获胜神经元的各连接权)按下式调整,其他神经元不变．

   $$\bf{IW} \it(k) = \bf{IW} \it(k - 1) + \alpha [p(k) - \bf{IW}\it( k - 1)]$$

   　　通过学习，那些最靠近输入向量的神经元权值向量的到修正，使之更靠近输入向量，结果是获胜的神经元在下一次相似的输入向量出现时，获胜的可能性会更大．经过大量的样本学习后，每一个网络层中的神经元权值向量很快被调整为最接近某一类输入向量的值．最终的结果是，如果神经元的数量足够多，则具有相似输入向量的各类模式作为输入向量时，其对应的神经元的输出为１，而对应于其他模式的输入向量，其对应的神经元输出为０．所以，竞争性神经网络具有对输入向量有学习分类的能力．

2. 阈值学习规则，以 learncon 实现阈值的修正

   　　竞争性神经网络的局限性在于可能有些神经元原理所有输入向量从而永远不会赢得竞争，这些神经元称为死神经元，他们实现不了任何函数映射．
   　　为避免这一现象的发生，对那些很少获胜的神经元赋以较大的阈值，对经常获胜的神经元赋以较小的阈值.
   　　算法如下

   $$c(k) = (1 - lr) \times c(k - 1) + lr \times a (k - 1)$$

   $$b(k) = exp[1 - \log{(c(k))}] - b (k - 1)$$

竞争型神经网络存在的问题

1. 学习模式样本本身杂乱无章，没有明显的分类特征时，网络对输入模式的相应呈现震荡．
2. 在权值和阈值的调整过程中，学习率的选择在收敛速度和稳定性间存在矛盾．
3. 网络的分类性能与权值和阈值的初值，学习率，训练样本的顺序训练次数都有关系，尚无有效方法评判．

程序设计

步骤

1. 创建竞争型神经网络．

   首先根据给定的问题确定训练样本的输入向量，当不足以区分各类模式时，应当增加特征值；其次是根据模式分类确定神经元的数目．

2. 训练网络

   训练最大次数默认是１００次，当训练结果不能满足分类的要求时，可尝试增加训练的次数

3. 以测试样本进行仿真

示例代码

clear all;

%% 定义输入向量
p = [0 0 0 1 1 1 -1 -1 -1;...
     0 1 -1 0 1 -1 0 1 -1;...
     1 1 10 10 1 1 1 10 1];

%% 创建竞争型网络
net = newc([-1 1; -1 1; 1 10], 2);

%% 训练神经网络
net = train(net, p);

save net net;

clear all;

%% 定义待测试样本输入向量
p = [0 0 0 1 1 1 -1 -1 -1;...
     0 1 -1 0 1 -1 0 1 -1;...
     1 1 10 10 1 1 1 10 1;];

load net net;

%% 网络仿真
y = sim(net, p);
% 仿真结果
yc = vec2ind(y);