B+ 树

发表于 更新于 分类于
结构及算法

　　B+ 树是基于 B 树的一种变形，B 树可以认为是 n 叉(N-ary)平衡树.
　　B+ 树中的每个结点可以有大量数目的子结点．一个 B+ 树由根结点，内部结点，和叶子结点组成，根结点可以是叶结点(此时树的高度只有 1 层)或者有多个孩子的结点.
　　一个 B+ 树可以看作为一个每个结点只有键(不是键值对)的 B 树，另外在最底层增加了一层相连的叶子层.
　　B+ 树的主要用处在于存储在块组织环境中的数据，特别是文件系统．这是因为 B+ 树与二叉树不同在于，B+ 树有非常大的扇出系数(一个结点的孩子结点数目，通常在 100 以上或更多)，这减少了找到一个树中的元素需要的 I/O 操作数目.

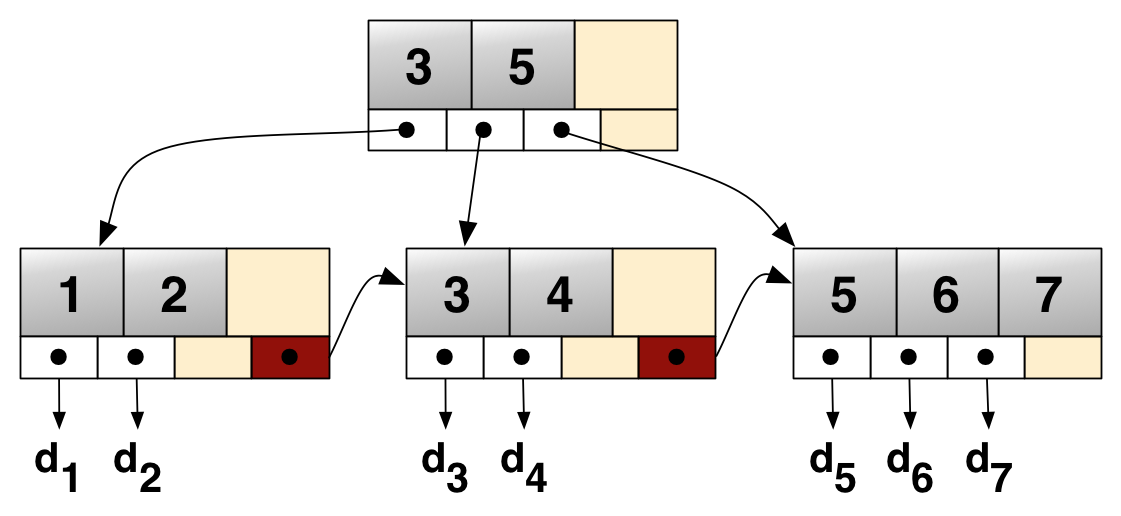
B_Plus_tree

　　以上这个简单的 B+ 树示例将键 1 - 7 连接到值 . 链表(红色)允许快速遍历叶子结点．这棵树的分支因子是 4.
　　B+ 树通常用于数据库和操作系统的文件系统中．B+ 树的特点是能够保持数据稳定有序，其插入与修改拥有较稳定的对数时间复杂度．B+ 树元素自底向上插入，这与二叉树恰好相反．

结点结构

　　B+ 树的序数(或者分支因子)决定了内部结点的容量(i.e. 孩子结点的数目).
　　假设一个结点的孩子结点数目为 , 内部结点的 值被约束为 . 根结点是个例外: 它最少可以有 2 个孩子结点．
　　示例: 如果一个 B+ 树的序数为 7, 每个内部结点(根结点除外)可以有 4 到 7 个孩子结点；根结点可以有 2 到 7 个孩子结点．叶结点没有孩子，但是它的键的数目被约束在 到 之间．当树几乎为空的时候，即这个树只有一个结点，这个结点允许最少含有一个键，最多仍然是 .
　　每个内部结点的元素充当其分开它的子树的分离值．例如，如果内部结点有三个子结点，则它必须有两个分离值或元素 和 . 在最左子树中所有的值都小于等于 , 在中间子树所有的值都在区间 , 最右子树中的所有值都大于

算法

查找

　　假设我们是在 B+ 树中查找值 K, 从根结点开始，我们查找一个可能包含 K 的叶子结点．在每个结点上，我们找出应该继续向下的结点．一个 B+ 树的内部结点可能包含 孩子结点，每个都代表了一个不同的子区间．我们选择所要查找的结点的键所在区间的结点．
　　在结点内部，典型的搜索方式是二分查找.

　　伪代码

1
2
3
4
5
6
7
8
9
10
11
12
Function: search(k)
    return tree_search(k, root)
Function: tree_search(k, node)
    if node is leaf then
        return node
    switch k do
    case k < k_0
        return tree_search(k, p_0)
    case k_i <= k < k_{i + 1}
        return tree_search(k, p_{i + 1})
    case k_d < k
        return tree_search(k, p_{d + 1})

插入

  • 执行搜索决定新的记录应该进入哪一个桶
  • 如果这个桶没有满(插入后最多包含 个条目), 插入这个新的记录
  • 否则，在插入新的记录前
    • 将结点分开
      • 原始结点包含 条目
      • 新结点包含
    • 将 键移动到父亲结点，将新结点加入到父结点中
    • 重复以上动作直到不需要在分割结点为止
  • 如果根结点被分割，将认为其有一个空父结点并按上面算法分割

删除

  • 从根结点开始，查找要删除的条目所在的叶子结点 L
  • 删除这个条目
    • 如果这个叶子的至少半满，那么工作完成
    • 如果叶子结点 L 所包含的条目数少于
      • 如果兄弟结点超过半满，重新分发条目，借用兄弟结点中的条目
      • 否则，兄弟结点刚好半满，我们就可以合并 L 和其兄弟结点
  • 如果发生了合并，必须从 L 的父结点中删除实体(L 或其兄弟结点)
  • 合并操作可以传播到根结点，降低高度